My research belongs to nonlinear dynamics, statistical physics, and related fields, focusing on the following three areas.

Nonlinear waves; Metamaterials; Nonlinear optics

I am interested in nonlinear waves in optical and mechanical metamaterials. A central theme is nonlinear edge waves in optical and mechanical topological insulators, and the overall goal is to elevate the functionalities of optical and mechanical devices using various combinations between topological science and nonlinear science. I am also interested in other types of nonlinear waves including domain walls, vector solitons, self-similar solutions, and dispersive shock waves, which arise in diverse settings including the coupled nonlinear Schrödinger equation, the hyperbolic nonlinear Schrödinger equation, the Kadomtsev-Petviashvili equation, and the 2D Benjamin-Ono equation.

Publications:

1. [DOI] D. D. J. M. Snee and Y.-P. Ma. Domain walls and vector solitons in the coupled nonlinear Schrödinger equation. Journal of Physics A 57 (3), 035702 (2024).
2. [DOI] Y.-P. Ma and H. Susanto. Topological edge solitons and their stability in a nonlinear Su-Schrieffer-Heeger model. Physical Review E 104, 054206 (2021).
3. [DOI] D. D. J. M. Snee and Y.-P. Ma. Edge solitons in a nonlinear mechanical topological insulator. Extreme Mechanics Letters 30, 100487 (2019).
4. [DOI] M. J. Ablowitz, Y.-P. Ma, and I. Rumanov. A universal asymptotic regime in the hyperbolic nonlinear Schrödinger equation. SIAM Journal on Applied Mathematics 77(4), 1248-1268 (2017).
5. [DOI] M. J. Ablowitz, A. Demirci, and Y.-P. Ma. Dispersive shock waves in the Kadomtsev-Petviashvili and Two Dimensional Benjamin-Ono equations. Physica D 333, 84-98 (2016).
6. [DOI] C. Chong, P. G. Kevrekidis, M. J. Ablowitz, and Y.-P. Ma. Conical wave propagation and diffraction in two-dimensional hexagonally packed granular lattices. Phys. Rev. E 93, 012909 (2016).
7. [DOI] M. J. Ablowitz and Y.-P. Ma. Strong transmission and reflection of edge modes in bounded photonic graphene. Opt. Lett. 40, 4635-4638 (2015).
8. [DOI] M. J. Ablowitz, C. W. Curtis, and Y.-P. Ma. Adiabatic dynamics of edge waves in photonic graphene. 2D Materials 2 (2), 024003 (2015).
9. [DOI] M. J. Ablowitz, C. W. Curtis, and Y.-P. Ma. Linear and nonlinear traveling edge waves in optical honeycomb lattices. Phys. Rev. A 90, 023813 (2014).

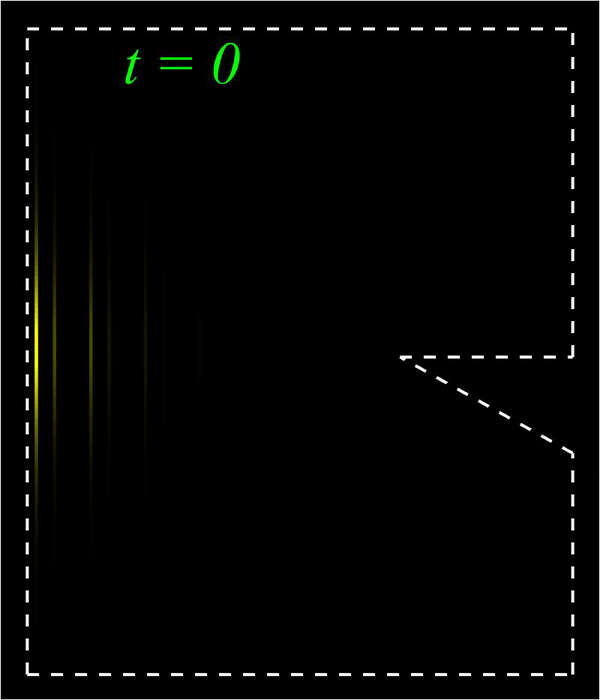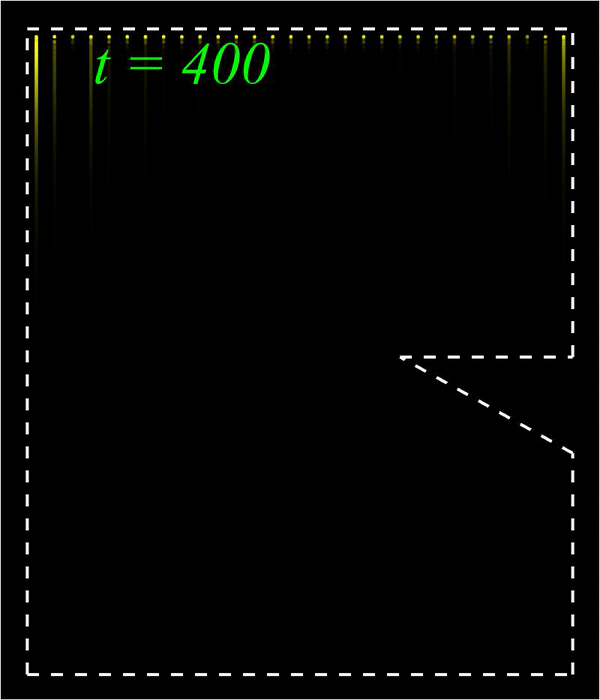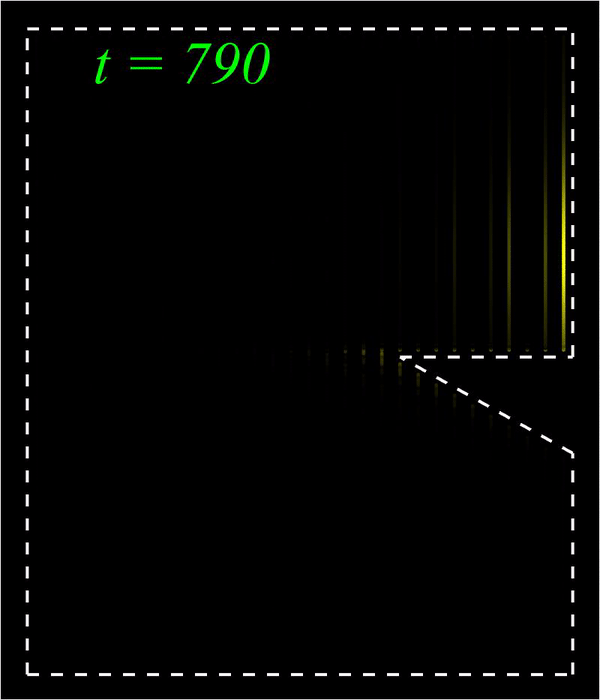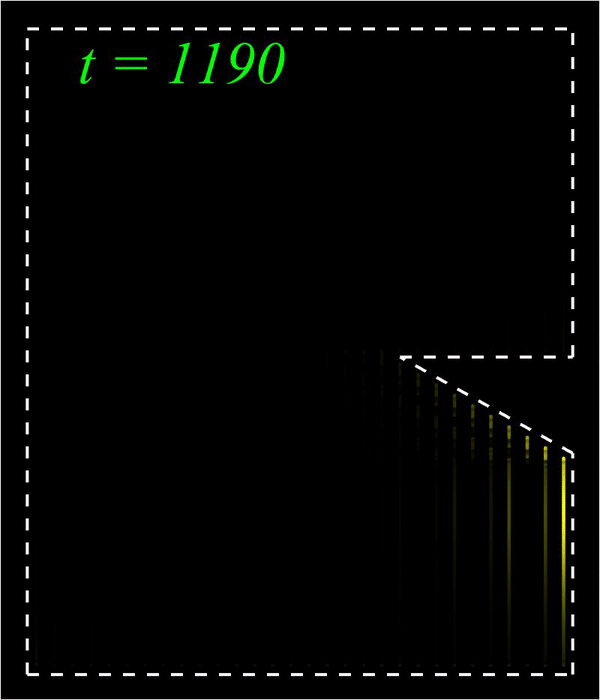
Bright (left) and Peregrine (right) edge solitons in a mechanical topological insulator.

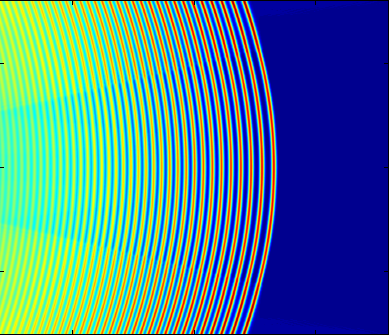
Dispersive shock waves in the Kadomtsev-Petviashvili (left) and 2D Benjamin-Ono (right) equations.

Climate dynamics; Statistical physics; Fluid mechanics

I am interested in meltwater patterns in cold environments, e.g., the polar regions. The overall goal is to construct efficient parametrization schemes for such ice-water mixtures using various models in the statistical physics of phase transitions, a prime example being an Ising model that explains the geometric characteristics of Arctic melt ponds. I am also interested in some branches of fluid mechanics including Rayleigh-Bénard convection. I have also worked on other applications of statistical physics including minority game and other problems in fluid mechanics including Homann stagnation-point flow.

Publications:

1. [DOI] Y.-P. Ma, I. Sudakov, C. Strong, and K. M. Golden. Ising model for melt ponds on Arctic sea ice. New Journal of Physics 21(6), 063029 (2019).
2. [DOI] P. Weidman and Y.-P. Ma. The competing effects of wall transpiration and stretching on Homann stagnation-point flow. Eur. J. Mech. B-Fluid 60, 237-241 (2016).
3. [DOI] Y.-P. Ma and E. A. Spiegel. A diagrammatic derivation of (convective) pattern equations. Physica D 240, 150-165 (2011).
4. [DOI] C.-H. Yeung, Y.-P. Ma, K. Y. M. Wong. Epoch lifetimes in the dynamics of a competing population. Int. J. Mod. Phys. B 21, 4048-4053 (2007).
5. [PDF] C.-H. Yeung, Y.-P. Ma and K. Y. M. Wong. Stable aggregates in the dynamics of a competing population. J. Korean Phys. Soc. 50, 196-200 (2007).

Metastable state in the random field Ising model (left) and aerial image of Arctic melt ponds (right).

Diagrams to derive the Swift-Hohenberg equation for Rayleigh-Bénard convection.

Pattern formation; Dynamical systems

I am interested in spatially localized states in driven dissipative systems, e.g., localized Turing patterns in forced oscillatory systems and Turing-Hopf localized states in the Brusselator model. The overall goal is to understand the interplay between the interface dynamics between two patterns and the intrinsic dynamics within each pattern. The prototypical solutions can be understood using spatial dynamics, i.e., dynamical systems methods in space rather than in time. I have also worked on other applications of dynamical systems including cooperation and free-riding in social science.

Publications:

1. [DOI] Y.-P. Ma and E. Knobloch. Two-dimensional localized structures in harmonically forced oscillatory systems. Physica D 337, 1-17 (2016).
2. [DOI] J. C. Tzou, Y.-P. Ma, A. Bayliss, B. J. Matkowsky, and V. A. Volpert. Homoclinic snaking near a codimension-two Turing-Hopf bifurcation point in the Brusselator model. Phys. Rev. E 87, 022908 (2013).
3. [DOI] A. R. Champneys, E. Knobloch, Y.-P. Ma and T. Wagenknecht. Homoclinic snakes bounded by a saddle-center periodic orbit. SIAM J. Appl. Dyn. Syst. 11(4), 1583-1613 (2012).
4. [DOI] Y.-P. Ma and E. Knobloch. Depinning, front motion and phase slips. Chaos 22, 033101 (2012).
5. [DOI] Y.-P. Ma, J. Burke and E. Knobloch. Defect-mediated snaking: A new growth mechanism for localized structures. Physica D 239, 1867-1883 (2010).
6. [DOI] Y.-P. Ma, S. Gonçalves, S. Mignot, J.-P. Nadal and M. B. Gordon. Cycles of cooperation and free-riding in social systems. Eur. Phys. J. B 71, 597-610 (2009).

2D localized hexagonal pattern in the 1:1 forced complex Ginzburg-Landau equation (FCGLE).

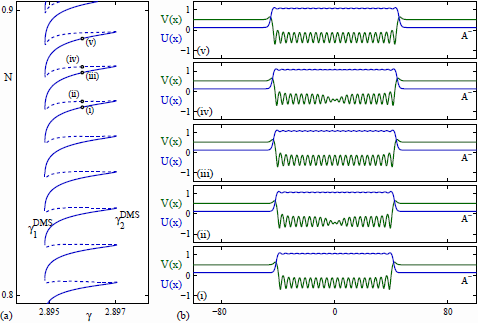
Defect-mediated snaking of 1D localized Turing patterns in the 1:1 FCGLE.